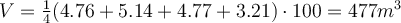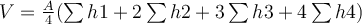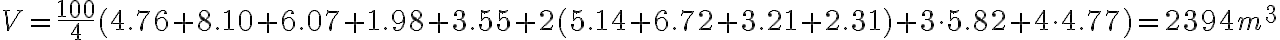Surveying ME - BMEEOAFM201

This method is typically applied when the original terrain is more or less linear and an earthwork is just a horizontal plane. A TIN-model is used to describe the original terrain. In the first step, a grid model is derived using linear interpolation. In the grid points, the difference between the terrain and the planned earthwork is computed. More dense the grid is, more accurate the result can be, however, more the amount of computation is.

The volume for each grid is computed as the multiplication of its area and its average depth value. The volume of total earthwork is computed as the sum of each grid volume.

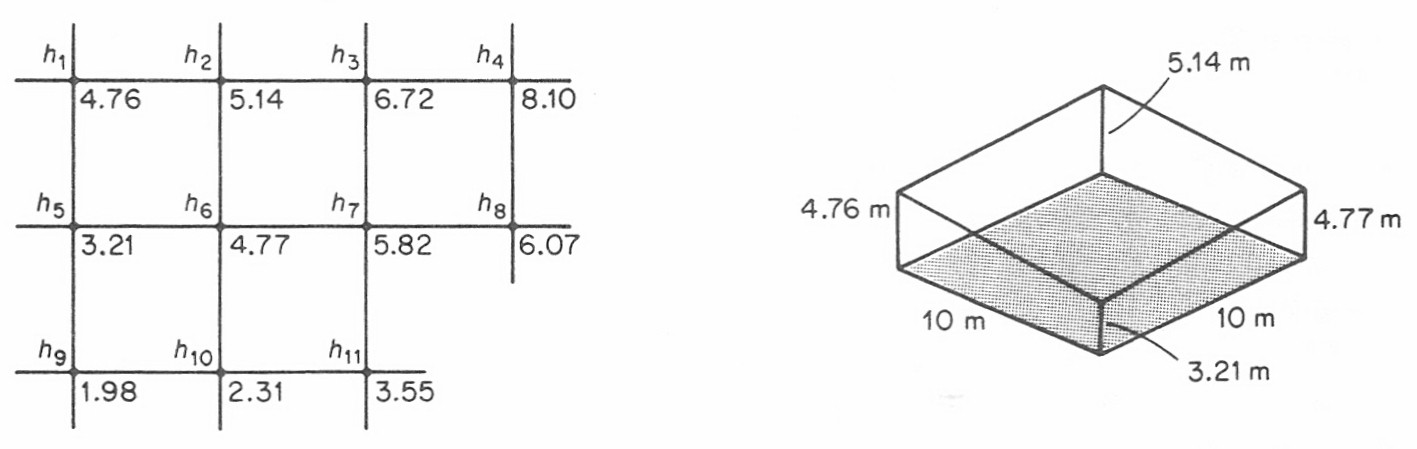
As you may see in the picture, the volume of the cell in the grid is:

$V= \frac{1}{4} (4.76 + 5.14 + 4.77 + 3.21) \cdot 100 = 477 m^3$

In general:

$V= \frac{A}{4} ( \sum{h1} + 2 \sum{h2} + 3\sum{h3} + 4 \sum{h4} )$

where

$A$ is the area of the cell

$h1$ depth in those grid points which are taken into account just once, like $h_1$

$h2$ depth in those grid points which are taken into account two times, like $h_2$

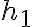
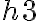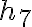
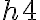$h3$ depth in those grid points which are taken into account three times, like $h_7$

$h4$ depth in those grid points which are taken into account four times, like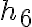 $h_6$

Volume according to the example in the picture is

$V= \frac{100}{4} (4.76+8.10+6.07+1.98+3.55+2(5.14+6.72+3.21+2.31)+3 \cdot5.82+ 4 \cdot4.77)= 2394m^3$

The example is taken from [Uren and Price, 1985].